Mass Luminosity Relationship
The study of binary stars provides the key piece of information to understanding why main sequence stars have a range of properties from high luminosity to low luminosity. Orbital periods and orbital radii via Kepler's Third Law yields the mass of stars. When the luminosity of main sequence stars is plotted against their masses, we observe a mass‐luminosity relationship, approximately of the form L ∝ M 3.5 (see Figure ). In other words, doubling the mass of a main sequence star produces an increase in luminosity by a factor 2 3.5 = 11 times. The Main Sequence is therefore a mass sequence, with low mass stars forming an equilibrium with a cool surface and a low luminosity (low energy generation rate), and high mass stars having hot surfaces and high luminosity (larger energy generation rate). The mass‐luminosity relation holds only for main sequence stars. Two giant or supergiant stars with the same luminosities and surface temperatures may have dramatically different masses.
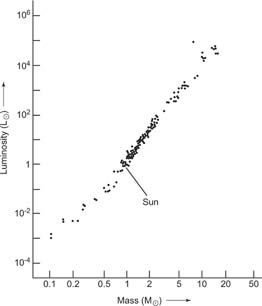
Figure 1
Mass-luminosity relationship for main sequence stars.
The fact that luminosity is not directly proportional to mass produces a major problem for observing and interpreting the universe. This problem can be seen by considering the masses, luminosities, and mass‐luminosity ratios M/L for different types of stars (only three types are considered in Table 1 for simplicity):
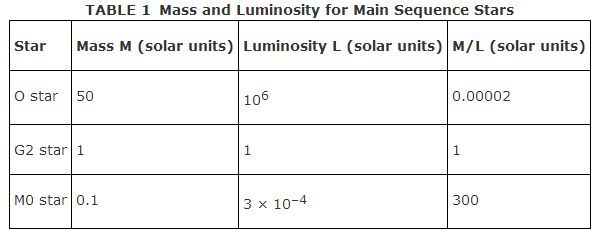
One million G2 stars like the Sun or three billion M0 stars produce the same amount of light as one O star. That one O star represents 50 solar masses of material, whereas the G2 stars would have a total of 1,000,000 solar masses and the M0 stars would have 300,000,000 solar masses. Even though hot, massive, luminous stars are rare, they can easily outshine the vast bulk of the more common stars. In almost any kind of stellar system (star cluster, galaxy), the light is dominated by that coming from only a small fraction of that mass, yet the real structure of any stellar system is represented by the distribution of its mass in space. The visible appearance of an object may actually be rather misleading in terms of what an object actually is.
The main sequence is bounded by upper and lower mass limits of about 80 solar masses and about 0.08 solar masses, respectively. Why should there not be more massive (and hence brighter) and less massive (hence fainter) stars? The upper limit ( Eddington limit) is set by radiation pressure in the star's photosphere. An 80 solar mass star is not that much bigger than the Sun, but its luminosity is 10 6 times greater. The radiation passing through each square meter of photosphere is perhaps 10 4 times greater than for the Sun. Radiation can apply a pressure (force per unit area) when it interacts with matter because photons of light can act as particles. In collisions with atoms, the atoms can be kicked away from the star. At the upper mass limit of main sequence stars, the addition of a bit more mass would increase the luminosity and radiative flux and simply blow away what has been added. Stable stars in a main sequence state with more than about 80 solar masses simply cannot exist.
The lower mass limit on stars seems to be about 0.08 solar masses. Below this mass limit, internal temperatures and pressures are too low to sustain thermonuclear conversion of hydrogen to helium. Without a thermonuclear energy source, an object is not self‐luminous. It would be what has been called a failed star. Such objects actually exist and radiate at infrared wavelengths due to their store of heat energy generated when they contracted gravitationally — these are termed brown dwarfs. Less massive objects are planetary bodies like Jupiter.