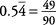Changing Infinite Repeating Decimals to Fractions
Remember: Infinite repeating decimals are usually represented by putting a line over (sometimes under) the shortest block of repeating decimals. Every infinite repeating decimal can be expressed as a fraction.
Find the fraction represented by the repeating decimal  .
.
Let n stand for  or 0.77777 …
or 0.77777 …
So 10 n stands for  or 7.77777 …
or 7.77777 …
10 n and n have the same fractional part, so their difference is an integer.
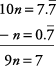
You can solve this problem as follows.
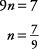
So 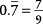
Find the fraction represented by the repeating decimal  .
.
Let n stand for  or 0.363636 …
or 0.363636 …
So 10 n stands for  or 3.63636 …
or 3.63636 …
and 100 n stands for  or 36.3636 …
or 36.3636 …
100 n and n have the same fractional part, so their difference is an integer. (The repeating parts are the same, so they subtract out.)
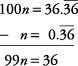
You can solve this equation as follows:
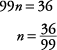
Now simplify  to
to  .
.
So 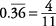
Find the fraction represented by the repeating decimal  .
.
Let n stand for  or 0.544444 …
or 0.544444 …
So 10 n stands for  or 5.444444 …
or 5.444444 …
and 100 n stands for  or 54.4444 …
or 54.4444 …
Since 100 n and 10 n have the same fractional part, their difference is an integer. (Again, notice how the repeated parts must align to subtract out.)
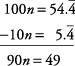
You can solve this equation as follows.
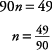
So