Populations, Samples, Parameters, and Statistics
The field of inferential statistics enables you to make educated guesses about the numerical characteristics of large groups. The logic of sampling gives you a way to test conclusions about such groups using only a small portion of its members.
A population is a group of phenomena that have something in common. The term often refers to a group of people, as in the following examples:
- All registered voters in Crawford County
- All members of the International Machinists Union
- All Americans who played golf at least once in the past year
But populations can refer to things as well as people:
- All widgets produced last Tuesday by the Acme Widget Company
- All daily maximum temperatures in July for major U.S. cities
- All basal ganglia cells from a particular rhesus monkey
Often, researchers want to know things about populations but do not have data for every person or thing in the population. If a company's customer service division wanted to learn whether its customers were satisfied, it would not be practical (or perhaps even possible) to contact every individual who purchased a product. Instead, the company might select a sample of the population. A sample is a smaller group of members of a population selected to represent the population. In order to use statistics to learn things about the population, the sample must be random. A random sample is one in which every member of a population has an equal chance of being selected. The most commonly used sample is a simple random sample. It requires that every possible sample of the selected size has an equal chance of being used.
A parameter is a characteristic of a population. A statistic is a characteristic of a sample. Inferential statistics enables you to make an educated guess about a population parameter based on a statistic computed from a sample randomly drawn from that population (see Figure 1).
Figure 1.Illustration of the relationship between samples and populations.

For example, say you want to know the mean income of the subscribers to a particular magazine—a parameter of a population. You draw a random sample of 100 subscribers and determine that their mean income is $27,500 (a statistic). You conclude that the population mean income μ is likely to be close to $27,500 as well. This example is one of statistical inference.
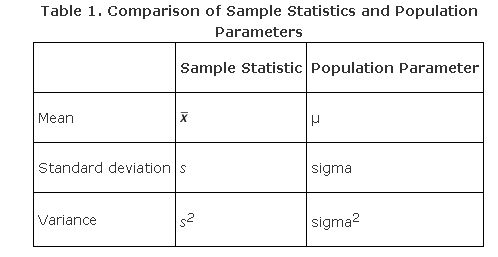
Different symbols are used to denote statistics and parameters, as Table 1 shows.
|
|
|