Kinematics in Two Dimensions

Our world is three‐dimensional. For easier analysis, many motions can be simplified to two dimensions. For example, an object fired into the air moves in a vertical, two‐dimensional plane; also, horizontal motion over the earth's surface is two‐dimensional for short distances. Elementary vector algebra is required to examine the relationships between vector quantities in two dimensions.

Addition and subtraction of vectors: geometric method

The vector A shown in Figure (a) represents a velocity of 10 m/s northeast, and vector B represents a velocity of 20 m/s at 30 degrees north of east. (A vector is named with a letter in boldface, nonitalic type, and its magnitude is named with the same letter in regular, italic type. You will often see vectors in the figures of the book that are represented by their magnitudes in the mathematical expressions.) Vectors may be moved over the plane if the represented length and direction are preserved.

Figure 1

Graphical addition of vectors, A + B = C.

In Figure (b), the same vectors are positioned to be geometrically added. The tail of one vector, in this case A, is moved to the head of the other vector ( B). The vector sum ( C) is the vector that extends from the tail of one vector to the head of the other. To find the magnitude of C, measure along its length and use the given scale to determine the velocity represented. To find the direction θ of C, measure the angle to the horizontal axis at the tail of C.

Figure (a) shows that A + B = B + A. The sum of the vectors is called the resultant and is the diagonal of a parallelogram with sides A and B. Figure (b) illustrates the construction for adding four vectors. The resultant vector is the vector that results in the one that completes the polygon.

Figure 2

(a) A + B = B + A. (b) Graphical addition of several vectors.

To subtract vectors, place the tails together. The difference of the two vectors ( D) is the vector that begins at the head of the subtracted vector ( B) and goes to the head of the other vector ( A). An alternate method is to add the negative of a vector, which is a vector with the same length but pointing in the opposite direction. The second method is demonstrated in Figure .

Figure 3

Graphical subtraction of vectors, A − B = D.

Addition and subtraction of vectors: Component method

For precision in adding vectors, an analytical method using basic trigonometry is required because scale drawings do not give accurate values.

Consider vector A in the rectangular coordinate system of Figure . The vector A can be expressed as the sum of two vectors along the x and y axes, A = A _x + A _y, where A _x and A _y are called the components of A. The direction of A _x is parallel to the x axis, and that of A _y is parallel to the y axis. The magnitudes of the components are obtained from the definitions of the sine and cosine of an angle: cos θ = A _x/ A and sin θ = A _y/ A, or

Figure 4

Components of a vector.

To add vectors numerically, first find the components of all the vectors. The signs of the components are the same as the signs of the cosine and sine in the given quadrant. Then, sum the components in the x direction, and sum the components in the y direction. As shown in Figure , the sum of the x components and the sum of the y components of the given vectors ( A and B) comprise the x and y components of the resultant vector ( C).

Figure 5

Component method of vector addition, A + B = C.

These resultant components form the two sides of a right angle with a hypotenuse of the magnitude of C; thus, the magnitude of the resultant is

The direction of the resultant ( C) is calculated from the tangent because tan θ = C _x/ C _y. To solve for the angle θ, use θ = tan ⁻¹ ( C _y/ C _x).

The procedure can be summarized as follows:

1. Sketch the vectors on a coordinate system.

2. Find the x and y components of all the vectors, with the appropriate signs.

3. Sum the components in both the x and y directions.

4. Find the magnitude of the resultant vector from the Pythagorean theorem.

5. Find the direction of the resultant vector using the tangent function.

Follow the same procedure to subtract vectors by calculating the appropriate algebraic sum of the components in Step 3.

Multiplication of vectors

The dot product: There are two different ways in which two vectors may be multiplied together. The first is the dot product, also called the scalar product, which is written A · B. This can be evaluated in two ways:

A · B = A _xB _x+ A _yB _y

A · B = AB cos θ, where θ is the angle between the vectors when they are set tail to tail, and A and B are the lengths of the vectors.

Note that the order of the vectors does not matter and that the result of the dot product is a scalar rather than a vector. Note that if two vectors are perpendicular, their dot product is zero according to the second rule above.

Cross product: The second way to multiply vectors is called the cross product or the vector product. It is written A · B. It can be evaluated in two ways:

A · B = ( A _xB _y− A _yB _xz, when the vectors A and B both are in x–y plane. The z indicates that the result is a vector that points along the z axis. In general, the vector resulting from a cross product is always perpendicular to both of the vectors being multiplied together.

A · B = AB z sin θ, where θ is the angle between the vectors A and B when they are placed tail to tail. Again, the result is a vector perpendicular to A and B (and therefore points along the z axis if A and B are in the x–y plane).

The result of a cross product does depend on the order of the vectors. Note from the first rule that A · B = − B · A. Also, if A and B are parallel, the second rule implies that their cross product is zero.

Finally, the cross product give rise to the “right hand rule,” which allows you to easily determine the direction of the resulting vector. For the general expression A × B = C, point your thumb in the direction of A. Now point your index finger in the direction of B; if necessary, flip over your hand. The vector C points outward from your palm.

Velocity and acceleration vectors in two dimensions

For motion in two dimensions, the earlier kinematics equations must be expressed in vector form. For example, the average velocity vector is v = ( d _f− d _o)/ t, where d _oand d _fare the initial and final displacement vectors and t is the time elapsed. As noted earlier, the velocity and displacement vectors are shown in bold type, whereas the scalar (t) is not. In similar fashion, the average acceleration vector is a = ( v _f− v _o)/ t, where v _oand v _fare the initial and final velocity vectors.

An important point is that the acceleration can arise from a change in the magnitude of the velocity (speed) as well as from a change in the direction of the velocity. If an object travels around a circle at a constant speed, there is an acceleration due to the change in the direction of the velocity, even though the magnitude of the velocity does not change. A mass moves in a horizontal circle with a constant speed in Figure . The velocity vectors at positions 1 and 2 are subtracted to find the average acceleration, which is directed toward the center of the circle. (Note that the average acceleration vector is placed at the midpoint of the path in the given time interval.)

Figure 6

Velocity and acceleration vectors of an object moving in a circle

The following discussion summarizes the four different cases for acceleration in a plane:

Case 1: Zero acceleration

Case 2: Acceleration due to changing direction but not speed

Case 3: Acceleration due to changing speed but not direction

Case 4: Acceleration due to changing both speed and direction.

Imagine a ball rolling on a horizontal surface that is illuminated by a stroboscopic light. Figure (a) shows the position of the ball at even intervals of time along a dotted path. Case 1 is illustrated in positions 1 through 3; the magnitude and direction of the velocity do not change (the pictures are evenly spaced and in a straight line), and therefore, there is no acceleration. Case 2 is indicated for positions 3 through 5; the ball has constant speed but changing direction, and therefore, an acceleration exists. Figure (b) illustrates the subtraction of v ₃ and v ₄ and the resulting acceleration toward the center of the arc. Case 3 occurs from positions 5 to 7; the direction of the velocity is constant, but the magnitude changes. The acceleration for this portion of the path is along the direction of motion. The ball curves from position 7 to 9, showing case 4; the velocity changes both direction and magnitude. In this case, the acceleration is directed nearly upward between 7 and 8 and has a component toward the center of the arc due to the change in direction of the velocity and a component along the path due to the change in the magnitude of the velocity.

Figure 7

(a) Path of a ball on a table. (b) Acceleration between points 3 and 4.

Projectile motion

Anyone who has observed a tossed object—for example, a baseball in flight—has observed projectile motion. To analyze this common type of motion, three basic assumptions are made: (1) acceleration due to gravity is constant and directed downward, (2) the effect of air resistance is negligible, and (3) the surface of the earth is a stationary plane (that is, the curvature of the earth's surface and the rotation of the earth are negligible).

To analyze the motion, separate the two‐dimensional motion into vertical and horizontal components. Vertically, the object undergoes constant acceleration due to gravity. Horizontally, the object experiences no acceleration and, therefore, maintains a constant velocity. This velocity is illustrated in Figure where the velocity components change in the y direction; however, they are all of the same length in the x direction (constant). Note that the velocity vector changes with time due to the fact that the vertical component is changing.

Figure 8

Projectile motion.

In this example, the particle leaves the origin with an initial velocity ( v _o), up at an angle of θ _o. The original x and y components of the velocity are given by v _x0= v _oand v _y0= v _osin θ _o.

With the motions separated into components, the quantities in the x and y directions can be analyzed with the one‐dimensional motion equations subscripted for each direction: for the horizontal direction, v _x= v _x0and x = v _x0t; for vertical direction, v _y= v _y0− gt and y = v _y0− (1/2) gt ², where x and y represent distances in the horizontal and vertical directions, respectively, and the acceleration due to gravity ( g) is 9.8 m/s ². (The negative sign is already incorporated into the equations.) If the object is fired down at an angle, the y component of the initial velocity is negative. The speed of the projectile at any instant can be calculated from the components at that time from the Pythagorean theorem, and the direction can be found from the inverse tangent on the ratios of the components:

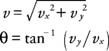
Other information is useful in solving projectile problems. Consider the example shown in Figure where the projectile is fired up at an angle from ground level and returns to the same level. The time for the projectile to reach the ground from its highest point is equal to the time of fall for a freely falling object that falls straight down from the same height. This equality of time is because the horizontal component of the initial velocity of the projectile affects how far the projectile travels horizontally but not the time of flight. Projectile paths are parabolic and, therefore, symmetric. Also for this case, the object reaches the top of its rise in half of the total time (T) of flight. At the top of the rise, the vertical velocity is zero. (The acceleration is always g, even at the top of the flight.) These facts can be used to derive the range of the projectile, or the distance traveled horizontally. At maximum height, v _y= 0 and t = T/2; therefore, the velocity equation in the vertical direction becomes 0 = v _osin θ − g T/2 or solving for T, T = (2 v ₀ sin θ)/ g.

Substitution into the horizontal distance equation yields R = ( v _ocos θ) T. Substitute T in the range equation and use the trigonometry identity sin 2θ = 2 sin θ cos θ to obtain an expression for the range in terms of the initial speed and angle of motion, R = ( v _o²/ g) sin 2θ. As indicated by this expression, the maximum range occurs when θ = 45 degrees because, at this value of θ, sin 2θ has its maximum value of 1. Figure sketches the trajectories of projectiles thrown with the same initial speed at differing angles of inclination.

Figure 9

Range of projectiles launched at different angles.

Uniform circular motion

For uniform motion of an object in a horizontal circle of radius (R), the constant speed is given by v = 2π R/ T, which is the distance of one revolution divided by the time for one revolution. The time for one revolution (T) is defined as period. During one rotation, the head of the velocity vector traces a circle of circumference 2π v in one period; thus, the magnitude of the acceleration is a = 2π v/ T. Combine these two equations to obtain two additional relationships in other variables: a = v ²/ R and a = (4π ²/ T ²) R.

The displacement vector is directed out from the center of the circle of motion. The velocity vector is tangent to the path. The acceleration vector directed to the center of the circle is called centripetal acceleration. Figure shows the displacement, velocity, and acceleration vectors at different positions as the mass travels in a circle on a frictionless horizontal plane.

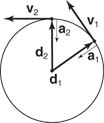
Figure 10

Uniform circular motion.

Physics