Physics

Magnetic fields and lines of force

A bar magnet attracts iron objects to its ends, called poles. One end is the north pole, and the other is the south pole. If the bar is suspended so that it is free to move, the magnet will align itself so that its north pole points to the geographic north of the earth. The suspended bar magnet acts like a compass in the earth's magnetic field. If two bar magnets are brought close together, the like poles will repel each other, and the unlike poles attract each other. ( Note: By this definition, the magnetic pole under the earth's north geographical pole is the south pole of the earth's magnetic field.)

This magnetic attraction or repulsion can be explained as the effect of one magnet on the other, or it can be said that one magnet sets up a magnetic field in the region around it that affects the other magnet. The magnetic field at any point is a vector. The direction of the magnetic field ( B) at a specified point is the direction that the north end of a compass needle points at that position. Magnetic field lines, analogous to electric field lines, describe the force on magnetic particles placed within the field. Iron filings will align to indicate the patterns of magnetic field lines.

Force on a moving charge

If a charge moves through a magnetic field at an angle, it will experience a force. The equation is given by F = q v × B or F = qvB sin θ, where q is the charge, B is the magnetic field, v is the velocity, and θ is the angle between the directions of the magnetic field and the velocity; thus, using the definition of the cross product, the definition for the magnetic field is

 

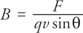
Magnetic field is expressed in SI units as a tesla (T), which is also called a weber per square meter: 

The direction of F is found from the right‐hand rule, shown in Figure 1.

Figure 1 Using the right-hand rule to find the direction of magnetic force on a moving charge.

To find the direction of the force on the charge, with a flat hand point your thumb in the direction of the velocity of the positive charge and your fingers in the direction of the magnetic field. The direction of the force is out of the palm of your hand. (If the moving charge is negative, point your thumb opposite to its direction of motion.) Mathematically, this force is the cross product of the velocity vector and the magnetic field vector.

If the velocity of the charged particle is perpendicular to the uniform magnetic field, the force will always be directed toward the center of a circle of radius r, as shown in Figure 2. The x symbolizes a magnetic field into the plane of the paper—the tail of the arrow. (A dot symbolizes a vector out of the plane of the paper—the tip of the arrow.)

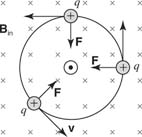
Figure 2 The force on a charge moving perpendicular to a magnetic field is toward the center of a circle.

The magnetic force provides centripetal acceleration: 

 

or

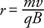
The radius of the path is proportional to the mass of the charge. This equation underlies the operation of a mass spectrometer, which can separate equally ionized atoms of slightly different masses. The singly ionized atoms are given equal velocities, and because their charges are the same and they travel through the same B, they will travel in slightly different paths and can then be separated.

Force on a current-carrying conductor

Charges confined to wires can also experience a force in a magnetic field. A current (I) in a magnetic field ( B) experiences a force ( F) given by the equation F = I l × B or F = IlB sin θ, where l is the length of the wire, represented by a vector pointing in the direction of the current. The direction of the force may be found by a right‐hand rule similar to the one shown in Figure . In this case, point your thumb in the direction of the current—the direction of motion of positive charges. The current will experience no force if it is parallel to the magnetic field.

Torque on a current loop

A loop of current in a magnetic field can experience a torque if it is free to turn. Figure (a) depicts a square loop of wire in a magnetic field directed to the right. Imagine in Figure (b) that the axis of the wire is turned to an angle (θ) with the magnetic field and that the view is looking down on the top of the loop. The x in a circle depicts the current traveling into the page away from the viewer, and the dot in a circle depicts the current out of the page toward the viewer.

Figure 3

(a) Square current loop in a magnetic field B. (b) View from the top of the current loop. (c) If the loop is tilted with respect to B, a torque results.

The right‐hand rule gives the direction of the forces. If the loop is pivoted, these forces produce a torque, turning the loop. The magnitude of this torque is t = NI A × B, where N is the number of turns of the loop, B is the magnetic field, I is the current, and A is the area of the loop, represented by a vector perpendicular to the loop.

Galvanometers, ammeters, and voltmeters

The torque on a current loop in a magnetic field provides the basic principle of the galvanometer, a sensitive current‐measuring device. A needle is affixed to a current coil—a set of loops. The torque gives a certain deflection of the needle, which is dependent upon the current, and the needle moves over a scale to allow a reading in amperes.

An ammeter is a current‐measuring instrument constructed from a galvanometer movement in parallel with a resistor. Ammeters are manufactured to measure different ranges of current. A voltmeter is constructed from a galvanometer movement in series with a resistor. The voltmeter samples a small portion of the current, and the scale provides a reading of potential difference—volts—between two points in the circuit.

Magnetic field of a long, straight wire

A current‐carrying wire generates a magnetic field of magnitude B in circles around the wire. The equation for the magnetic field at a distance r from the wire is

   

where I is the current in the wire and μ (the Greek letter mu) is the proportionality constant. The constant, called the permeability constant, has the value

The direction of the field is given by a second right‐hand rule, shown in Figure 4.

Figure 4 Using the second right-hand rule to determine the direction of the magnetic field resulting from a current.

Grasp the wire so that your thumb points in the direction of the current. Your fingers will curl around the wire in the direction of the magnetic field.

Ampere's law

Ampere's law allows the calculation of magnetic fields. Consider the circular path around the current shown in Figure . The path is divided into small elements of length (Δ l). Note the component of B that is parallel to Δ l and take the product of the two to be B _∥Δ l. Ampere's law states that the sum of these products over the closed path equals the product of the current and μ

Or in integral form, 

Somewhat analogous to the way Gauss's law can be used to find the electric field for highly symmetric charge configurations, Ampere's law can be used to find the magnetic fields for current configurations of high symmetry. For example, Ampere's law can be used to derive the expression for the magnetic field generated by a long, straight wire:

 

Magnetic fields of the loop, solenoid, and toroid

A current generates a magnetic field, and the field differs as the current is shaped into (a) a loop, (b) a solenoid (a long coil of wire), or (c) a toroid (a donut‐shaped coil of wire). The equations for the magnitudes of these fields follow. The direction of the field in each case can be found by the second right‐hand rule. Figure 5 illustrates the fields for these three different configurations.

Figure 5 Magnetic field resulting from (a) a current loop, (b) a solenoid, and (c) a toroid.

a. The field at the center of a single loop is given by

where r is the radius of the loop.

b. The field due to a solenoid is given by B = μ ₀ NI, where N is the number of turns per unit length.

c. The field due to a toroid is given by

where R is the radius to the center of the toroid.