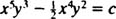Integrating Factors

If a differential equation of the form

is not exact as written, then there exists a function μ( x,y) such that the equivalent equation obtained by multiplying both sides of (*) by μ,

is exact. Such a function μ is called an integrating factor of the original equation and is guaranteed to exist if the given differential equation actually has a solution. Integrating factors turn nonexact equations into exact ones. The question is, how do you find an integrating factor? Two special cases will be considered.

Case 1:

Consider the differential equation M dx + N dy = 0. If this equation is not exact, then M _ywill not equal N _x; that is, M _y– N _x ≠ 0. However, if

is a function of x only, let it be denoted by ξ( x). Then

will be an integrating factor of the given differential equation.

Case 2:

Consider the differential equation M dx + N dy = 0. If this equation is not exact, then M _y will not equal N _x; that is, M _y – N _x≠ 0. = 0. However, if

is a function of y only, let it be denoted by ψ( y). Then

will be an integrating factor of the given differential equation.

Example 1: The equation

is not exact, since

However, note that

is a function of x alone. Therefore, by Case 1,

will be an integrating factor of the differential equation. Multiplying both sides of the given equation by μ = x yields

which is exact because

Solving this equivalent exact equation by the method described in the previous section, M is integrated with respect to x,

and N integrated with respect to y:

(with each “constant” of integration ignored, as usual). These calculations clearly give

as the general solution of the differential equation.

Example 2: The equation

is not exact, since

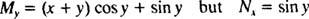
However, note that

is a function of y alone (Case 2). Denote this function by ψ( y); since

the given differential equation will have

as an integrating factor. Multiplying the differential equation through by μ = (sin y) ⁻¹ yields

which is exact because

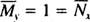
To solve this exact equation, integrate M with respect to x and integrate N with respect to y, ignoring the “constant” of integration in each case:

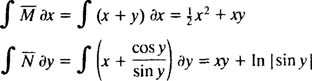
These integrations imply that

is the general solution of the differential equation.

Example 3: Solve the IVP

The given differential equation is not exact, since

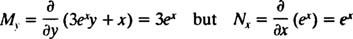
However, note that

which can be interpreted to be, say, a function of x only; that is, this last equation can be written as ξ( x) ≡ 2. Case 1 then says that

will be an integrating factor. Multiplying both sides of the differential equation by μ( x) = e ^{2 x}yields

which is exact because

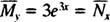
Now, since

and

(with the “constant” of integration suppressed in each calculation), the general solution of the differential equation is

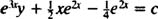
The value of the constant c is now determined by applying the initial condition y(0) = 1:

Thus, the particular solution is

which can be expressed explicitly as

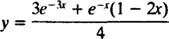
Example 4: Given that the nonexact differential equation

has an integrating factor of the form μ( x,y) = x ^ay ^bfor some positive integers a and b, find the general solution of the equation.

Since there exist positive integers a and b such that x ^ay ^bis an integrating factor, multiplying the differential equation through by this expression must yield an exact equation. That is,

is exact for some a and b. Exactness of this equation means

By equating like terms in this last equation, it must be the case that

The simultaneous solution of these equations is a = 3 and b = 1.

Thus the integrating factor x ^ay ^bis x ³ y, and the exact equation M dx + N dy = 0 reads

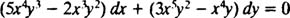
Now, since

and

(ignoring the “constant” of integration in each case), the general solution of the differential equation (*)—and hence the original differential equation—is clearly

Differential Equations

Integrating Factors