Cauchy‐Euler Equidimensional Equation
The second‐order homogeneous Cauchy‐Euler equidimensional equation has the form

where a, b, and c are constants (and a ≠ 0). The quickest way to solve this linear equation is to is to substitute y = x m and solve for m. If y = x m , then

so substitution into the differential equation yields
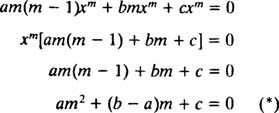
Just as in the case of solving second‐order linear homogeneous equations with constant coefficients (by first setting y = e mx and then solving the resulting auxiliary quadratic equation for m), this process of solving the equidimensional equation also yields an auxiliary quadratic polynomial equation. The question here is, how is y = x m to be interpreted to give two linearly independent solutions (and thus the general solution) in each of the three cases for the roots of the resulting quadratic equation?
Case 1: The roots of (*) are real and distinct.
If the two roots are denoted m 1 and m 2, then the general solution of the second‐order homogeneous equidimensional differ‐ential equation in this case is
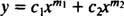
Case 2: The roots of (*) are real and identical.
If the double (repeated) root is denoted simply by m, then the general solution (for x > 0) of the homogeneous equidimensional differential equation in this case is
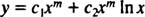
Case 3: The roots of (*) are distinct conjugate complex numbers.
If the roots are denoted r ± si, then the general solution of the homogeneous equidimensional differential equation in this case is
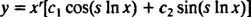
Example 1: Give the general solution of the equidimensional equation
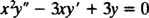
Substitution of y = x m results in
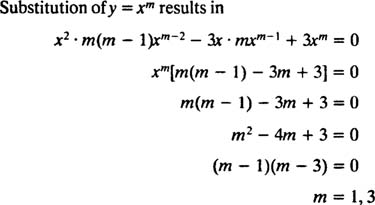
Since the roots of the resulting quadratic equation are real and distinct (Case 1), both y = x 1 = x and y = x 3 are solutions and linearly independent, and the general solution of this homogeneous equation is
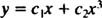
Example 2: For the following equidimensional equation, give the general solution which is valid in the domain x > 0:
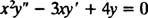
Substitution of y = x m

Since the roots of the resulting quadratic equation are real and identical (Case 2), both y = x 2 and y = x 2 In x are (linearly independent) solutions, so the general solution (valid for x > 0) of this homogeneous equation is
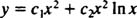
If the general solution of a nonhomogeneous equidimensional equation is desired, first use the method above to obtain the general solution of the corresponding homogeneous equation; then apply variation of parameters.