A Category 2 or Category 3 power series in x defines a function f by setting

for any x in the series' interval of convergence.
The power series expansion for f( x) can be differentiated term by term, and the resulting series is a valid representation of f′( x) in the same interval:

Differentiating again gives

and so on. Substituting

and in general, substituting x = 0 in the power series expansion for the nth derivative of f yields

These are called the Taylor coefficients of f, and the resulting power series

is called the Taylor series of the function f.
Given a function f, its Taylor coefficients can be computed by the simple formula above, and the question arises, does the Taylor series of f actually converge to f( x)? If it does, that is, if

for all x in some neighborhood of (interval around) 0, then the function f is said to be analytic (at 0). [More generally, if you form the Taylor series of f about a point x = x 0,

and if this series actually converges to f( x) for all x in some neighborhood of x 0, then f is said to be analytic at x 0.] Polynomials are analytic everywhere, and rational functions (quotients of polynomials) are analytic at all points where the denominator is not zero. Furthermore, the familiar transcendental (that is, nonalgebraic) functions e x , sin x, and cos x are also analytic everywhere. The Taylor series in Table 1 are encountered so frequently that they are worth memorizing.
For a general power series, it is usually not possible to express it in closed form in terms of familiar functions.
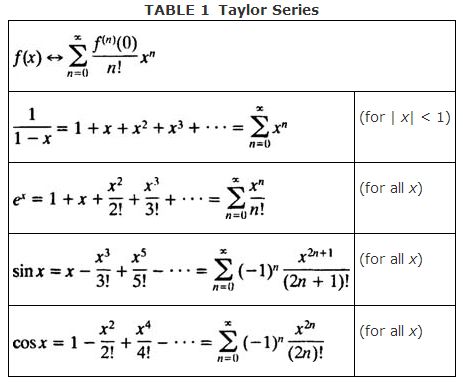
Example 1: Use Table 1 to find the Taylor series expansion of each of the following functions:
a. 
b. 
c. In(1 + x)
d. e − x 2
e. x cos x
f. sin x cos x
g. arctan x
a. Replacing x by x 2 in the Taylor series expansion of 1/(1 – x) gives

since | x| < 1 is equivalent to | x 2| < 1.
b. Differentiating 1/(1 – x) gives 1/(1 – x) 2, so differentiating the Taylor series expansion of 1/(1 – x) term by term will give the series expansion of 1/(1 – x) 2:

c. First, replacing x by − x in the Taylor series expansion of 1/(1 – x) gives the expansion of 1/(1 + x):

Now, since integrating 1/(1 + x) yields In(1 + x), integrating the Taylor series for 1/(1 + x) term by term gives the expansion for In(1 + x), valid for | x| < 1:

Technical note: Integrating 1/(1 + x) yields In (1 + x) + c (where c is some arbitrary constant), so strictly speaking, the equation above should have been written

However, substituting x = 0 into this equation shows that c = 0, so the expansion given above for In (1 + x) is indeed correct.
d. Replacing x by – x 2 in the Taylor series expansion of e x yields the desired result:

e. Multiplying each term of the Taylor series for cos x by x gives

f. One way to find the series expansion for sin x cos x is to multiply the expansions of sin x and cos x. A faster way, however, involves recalling the trigonometric identity sin 2 x = 2 sin x cos x and then replacing x by 2 x in the series expansion of sin x:

g. Since arctan x is the integral of 1/(1 + x 2), integrate the series expansion of 1/(1 + x 2) term by term:

Recall the technical note accompanying part c which also involved the term‐by‐term integration of a power series). The integral of 1/(1 + x 2) is actually arctan x + c, and the equation above should read

However, substituting x = 0 into this equation shows that c = 0, so the expansion given above for arctan x is indeed correct.