The Laplace Transform Operator

A particular kind of integral transformation is known as the Laplace transformation, denoted by L. The definition of this operator is

The result—called the Laplace transform of f—will be a function of p, so in general,

Example 1: Find the Laplace transform of the function f( x) = x.

By definition,

Integrating by parts yields

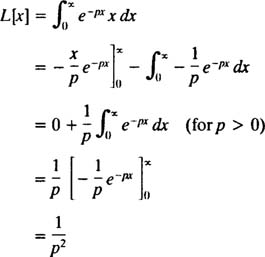
Therefore, the function F( p) = 1/ p ² is the Laplace transform of the function f( x) = x. [Technical note: The convergence of the improper integral here depends on p being positive, since only then will ( x/p) e ^{− px}and e ^{− px}approach a finite limit (namely 0) as x → ∞. Therefore, the Laplace transform of f( x) = x is defined only for p > 0.]

In general, it can be shown that for any nonnegative integer n,

Like the operators D and I—indeed, like all operators—the Laplace transform operator L acts on a function to produce another function. Furthermore, since

and

the Laplace transform operator L is also linear.

[Technical note: Just as not all functions have derivatives or integrals, not all functions have Laplace transforms. For a function f to have a Laplace transform, it is sufficient that f( x) be continuous (or at least piecewise continuous) for x ≥ 0 and of exponential order (which means that for some constants c and λ, the inequality holds for all x). Any bounded function (that is, any function f that always satisfies | f( x)| ≤ M for some M ≥ 0) is automatically of exponential order (just take c = M and λ = 0 in the defining inequality). Therefore, sin kx and cos kx each have a Laplace transform, since they are continuous and bounded functions. Furthermore, any function of the form e ^kx, as well as any polynomial, is continuous and, although unbounded, is of exponential order and therefore has a Laplace transform. In short, most of the functions you are likely to encounter in practice will have Laplace transforms.]

Example 2: Find the Laplace transform of the function f( x) = x ³ – 4 x + 2.

Recall form the first statement following Example 1 that the Laplace transform of f( x) = x ⁿis F( p) = n!/ p ^{n + 1}. Therefore, since the Laplace transform operator L is linear,

Example 3: Determine the Laplace transform of f( x) = e ^kx.

Apply the definition and perform the integration:

In order for this improper integral to converge, the coefficient ( p – k) in the exponential must be positive (recall the technical note in Example 1). Thus, for p > k, the calculation yields

Example 4: Find the Laplace transform of f( x) = sin kx.

By definition,

This integral is evaluated by performing integration by parts twice, as follows:

Therefore,

for p > 0. By a similar calculation, it can be shown that

Example 5: Determine the Laplace transform of the function

pictured in Figure 1:

Figure 1

This is an example of a step function. It is not continuous, but it is piecewise continuous, and since it is bounded, it is certainly of exponential order. Therefore, it has a Laplace transform.

Table 1 assembles the Laplace transforms of a few of the most frequently encountered functions, as well as some of the important properties of the Laplace transform operator L.

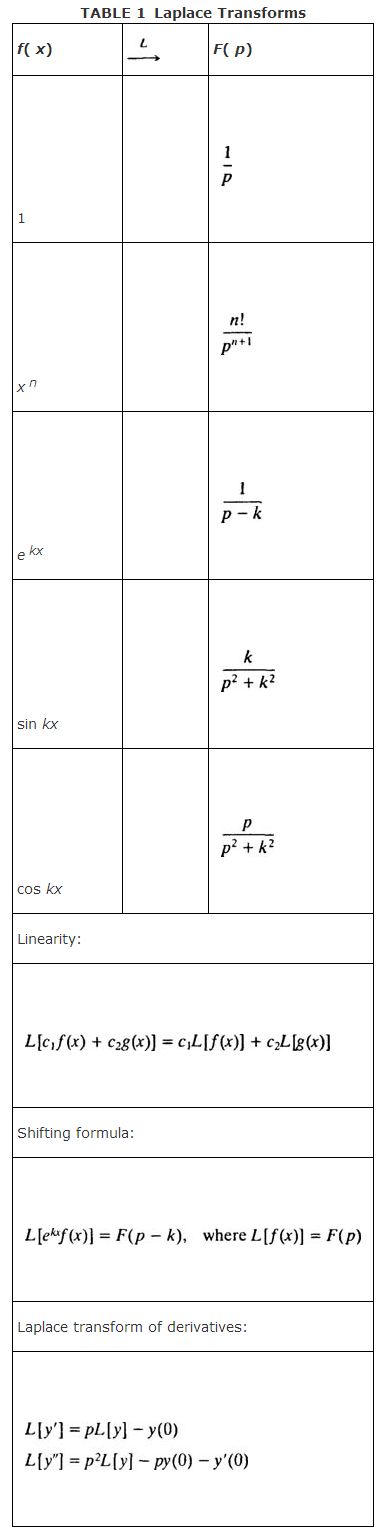
Example 6: Use Table 1 to find the Laplace transform of f( x) = sin ² x.

Invoking the trigonometric identity

linearity of L implies

Example 7: Use Table 1 to find the Laplace transform of g( x) x ³ e ^5x.

The presence of the factor e ^5x suggests using the shifting formula with k = ₅. Since

the shifting formula says that the Laplace transform of f( x) e ^5x = x ³ e ^5xis equal to F( P – 5). In other words, the Laplace transform of x ³ e ^5x is equal to the Laplace transform of x ³ with the argument p shifted to p – 5:

Example 8: Use Table 1 to find Laplace transform of f( x) = e ^−2x sin x – 3.

First, since L [sin x] = 1/( p ² + 1), the shifting formula (with k = −2) says

Now, because L[3] = 3 · L[1] = 3/ p, linearity implies

Example 9: Use Table 1 to find a continuous function whose Laplace transform is F( p) = 12/ p ⁵.

This example introduces the idea of the inverse Laplace transform operator,, L ⁻¹. The operator L ⁻¹ will “un‐do” the action of L. Symbolically,

If you think of the operator L as changing f( x) into F( p), then the operator L ⁻¹ just changes F( P) back into f( x). Like L, the inverse operator L ⁻¹ is linear.

More formally, the result of applying L ⁻¹ a function F( p) is to recover the continuous function f( x) whose Laplace transform is the given F( p). [This situation should remind remind you of the operators D and I (which are, basically, inverses of one another). Each will un‐do the action of the other in the sense that if, say, I changes f( x) into F( x), then D will change F( x) back into f( x). In other words, D = I ⁻¹, so if you apply I and then D, you're back where you started.]