The converse of this theorem is also true.
GH = 8 (Theorem 79)
Some additional theorems about chords in a circle are presented below without explanation. These theorems can be used to solve many types of problems.
Theorem 80: If a diameter is perpendicular to a chord, then it bisects the chord and its arcs.
In Figure 3, UT, diameter QS is perpendicular to chord QS By Theorem 80, QR = RS, m  = m
= m  , and m
, and m  = m
= m  .
.

Figure 3 A diameter that is perpendicular to a chord.
Theorem 81: In a circle, if two chords are equal in measure, then they are equidistant from the center.
In Figure 4, if AB = CD, then by Theorem 81, OX = OY.

Figure 4 In a circle, the relationship between two chords being equal in measure and being equidistant from the center.
Theorem 82: In a circle, if two chords are equidistant from the center of a circle, then the two chords are equal in measure.
In Figure 5, if OX = OY, then by Theorem 82, AB = CD.
Example 2: Use Figure to find x.
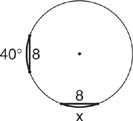
Figure 5 A circle with two minor arcs equal in measure.
Example 3: Use Figure 6, in which m  = 115°, m
= 115°, m  = 115°, and BD = 10, to find AC.
= 115°, and BD = 10, to find AC.
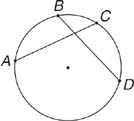
Figure 6 A circle with two minor arcs equal in measure.
Example 4: Use Figure 7, in which AB = 10, OA = 13, and m ∠ AOB = 55°, to find OM, m  and m
and m  .
.
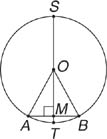
Figure 7 A circle with a diameter perpendicular to a chord.
So, ST ⊥ AB, and ST is a diameter. Theorem 80 says that AM = BM. Since AB = 10, then AM = 5. Now consider right triangle AMO. Since OA = 13 and AM = 5, OM can be found by using the Pythagorean Theorem.
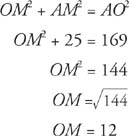
Also, Theorem 80 says that m  = m
= m  and m
and m  = m
= m  . Since m ∠ AOB = 55°, that would make m
. Since m ∠ AOB = 55°, that would make m  = 55° and m
= 55° and m  = 305°. Therefore, m
= 305°. Therefore, m  = 27 ½ and m
= 27 ½ and m  = 152 ½°.
= 152 ½°.
Example 5: Use Figure 8, in which AB = 8, CD = 8, and OA = 5, to find ON.
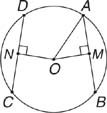
Figure 8 A circle with two chords equal in measure.
By Theorem 81, ON = OM. By Theorem 80, AM = MB, so AM = 4. OM can now be found by the use of the Pythagorean Theorem or by recognizing a Pythagorean triple. In either case, OM = 3. Therefore, ON = 3.