Figure 1 shows Δ ABC with D and E as midpoints of sides AC and AB respectively. If you look at this triangle as though it were a trapezoid with one base of BC and the other base so small that its length is virtually zero, you could apply the “median” theorem of trapezoids, Theorem 55.

Figure 1 The segment joining the midpoints of two sides of a triangle.
Theorem 56 (Midpoint Theorem): The segment joining the midpoints of two sides of a triangle is parallel to the third side and half as long as the third side.
In Figure 1, by Theorem 56,
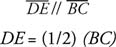
Example 1: In Figure 2, find HJ.

Figure 2 Compute the length of the broken line segment joining the midpoints of two sides of the triangle.
Because H and J are midpoints of two sides of a triangle:
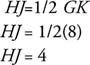
True or False: All triangles are convex
What is the degree measure of the interior angle determined by two adjacent sides of a regular decagon?
144°