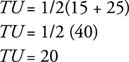Recall that the median of a trapezoid is a segment that joins the midpoints of the nonparallel sides.
Theorem 55: The median of any trapezoid has two properties: (1) It is parallel to both bases. (2) Its length equals half the sum of the base lengths.
In trapezoid ABCD (Figure 3) with bases AB and CD , E the midpoint of AD , and F the midpoint of BC , by Theorem 55:

Figure 3 A trapezoid with its median.
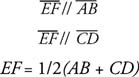
Example 1: In Figure 4, find m ∠ ABC and find BD.

Figure 4 An isosceles trapezoid with a specified angle and a specified diagonal.
m ∠ ABC = 120°, because the base angles of an isosceles trapezoid are equal.
BD = 8, because diagonals of an isosceles trapezoid are equal.
Example 2: In Figure 5, find TU.

Figure 5 A trapezoid with its two bases given and the median to be computed.
Because the median of a trapezoid is half the sum of the lengths of the bases: