Use Theorem 23:
Use Theorem 24:
Example 1: Using Figure 3, identify the given angle pairs as alternate interior, alternate exterior, consecutive interior, consecutive exterior, corresponding, or none of these: ∠1 and ∠7, ∠2 and ∠8, ∠3 and ∠4, ∠4 and ∠8, ∠3 and ∠8, ∠3, and ∠2, ∠5 and ∠7.
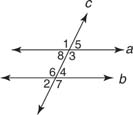
Figure 3 Find the angle pairs that are alternate interior, alternate exterior,
consecutive interior, consecutive exterior, and corresponding.
∠1 and ∠7 are alternate exterior angles.
∠2 and ∠8 are corresponding angles.
∠3 and ∠4 are consecutive interior angles.
∠4 and ∠8 are alternate interior angles.
∠3 and ∠2 are none of these.
∠5 and ∠7 are consecutive exterior angles.
Example 2: For each of the figures in Figure 4, determine which postulate or theorem you would use to prove l // m.
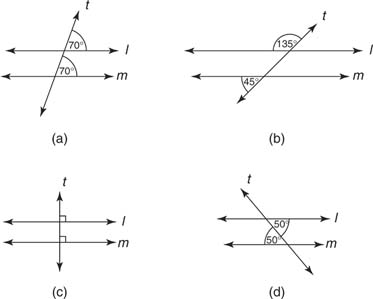
Figure 4 Conditions guaranteeing that lines l and m are parallel.
Figure 4 (a): If two lines and a transversal form equal corresponding angles, then the lines are parallel (Postulate 12).
Figure 4 (b): If two lines and a transversal form consecutive exterior angles that are supplementary, then the lines are parallel (Theorem 22).
Figure 4 (c): In a plane, if two lines are perpendicular to the same line, the two lines are parallel (Theorem 24).
Figure 4 (d): If two lines and a transversal form equal alternate interior angles, then the lines are parallel (Theorem 19).
Example 3: In Figure 5, a // b and m ∠1 = 117°. Find the measure of each of the numbered angles.
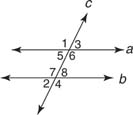
Figure 5 When lines a and b are parallel, knowing one angle makes it possible to determine
all the others pictured here.
m ∠2 = 63°
m ∠3 = 63°
m ∠4 = 117°
m ∠5 = 63°
m ∠6 = 117°
m ∠7 = 117°
m ∠8 = 63°