A prism shaped solid whose bases are circles is a cylinder. If the segment joining the centers of the circles of a cylinder is perpendicular to the planes of the bases, the cylinder is a right circular cylinder. In Figure 1, cylinder (a) is a right circular cylinder and cylinder (b) is an oblique circular cylinder.

Figure 1 Different types of circular cylinders.
Lateral area, total area, and volume for right circular cylinders are found in the same way as they are for right prisms.
If a cylinder is pictured as a soup can, its lateral area is the area of the label. If the label is carefully peeled off, the label becomes a rectangle, as shown in Figure 2.

Figure 2 The lateral area of a cylinder.
The area of the label is the area of a rectangle with a height the same as the altitude of the can and a base the same as the circumference of the lid of the can.
Theorem 90: The lateral area, LA, of a right circular cylinder with a base circumference C and an altitude h is given by the following equation.
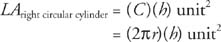
Theorem 91: The total area, TA, of a right circular cylinder with lateral area LA and a base area B is given by the following equation.
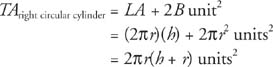
Theorem 92: The volume of a right circular cylinder, V, with a base area B and altitude h is given by the following equation.
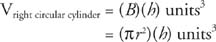
Example 1: Figure 3 is a right circular cylinder; find (a) LA (b) TA and (c) V.

Figure 3 Finding the lateral area, total area, and volume of a right circular cylinder.
