To find AC, though, simply subtracting is not sufficient. Triangle ABC is a right triangle with AC the hypotenuse. Therefore, by the Pythagorean Theorem,
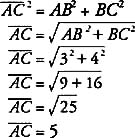
If A is represented by the ordered pair ( x 1, y 1) and C is represented by the ordered pair ( x 2, y 2), then AB = ( x 2 − x 1) and BC = ( y 2 − y 1).
Then
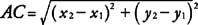
This is stated as a theorem.
Theorem 101: If the coordinates of two points are ( x 1, y 1) and ( x 2, y 2), then the distance, d, between the two points is given by the following formula (Distance Formula).
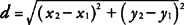
Example 1: Use the Distance Formula to find the distance between the points with coordinates (−3, 4) and (5, 2).
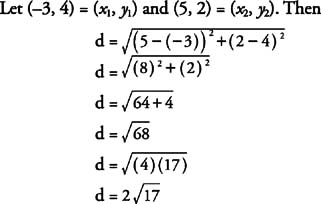
Example 2: A triangle has vertices A(12,5), B(5,3), and C(12, 1). Show that the triangle is isosceles.
By the Distance Formula,
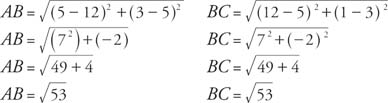
Because AB = BC, triangle ABC is isosceles.