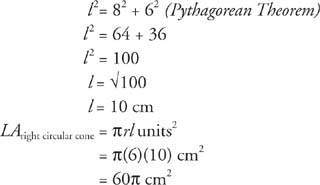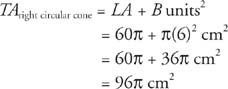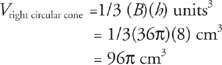A right circular cone is similar to a regular pyramid except that its base is a circle. The vocabulary and equations pertaining to the right circular cone are similar to those for the regular pyramid. Refer to Figure 1 for the vocabulary regarding right circular cones.

Figure 1 A right circular cone.
Theorem 96: The lateral area, LA, of a right circular cone with base circumference C and slant height l is given by the following equation.
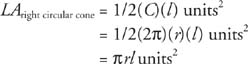
Theorem 97: The total area, TA, of a right circular cone with lateral area LA and base area B is given by the following equation.
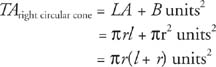
Theorem 98: The volume, V, of a right circular cone with base area B and altitude h is given by the following equation.
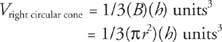
Example 1: Figure 2 is a right circular cone; find (a) LA (b) TA and (c) V.

Figure 2 Finding the lateral area, total area, and volume of a right circular cone.
The slant height, radius, and altitude of a right circular cone form a right triangle, as shown in Figure 3.

Figure 3 The right triangle formed by the slant height, radius, and altitude of a right circular cone.