Numerically, the midpoint of a segment can be considered to be the average of its endpoints. This concept helps in remembering a formula for finding the midpoint of a segment given the coordinates of its endpoints. Recall that the average of two numbers is found by dividing their sum by two.
Theorem 102: If the coordinates of A and B are ( x 1, y 1) and ( x 2, y 2) respectively, then the midpoint, M, of AB is given by the following formula (Midpoint Formula).
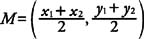
Example 1: In Figure 1, R is the midpoint between Q(−9, −1) and T(−3, 7). Find its coordinates and use the Distance Formula to verify that it is in fact the midpoint of QT .

Figure 1 Finding the coordinates of the midpoint of a line segment.
By the Midpoint Formula,
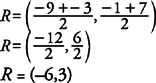
By the Distance Formula,
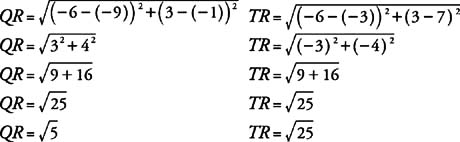
Because QR = TR and Q, T, and R are collinear, R is the midpoint of QT
Example 2: If the midpoint of AB is (−3, 8) and A is (12, −1), find the coordinates of B.
Let the coordinates of B be ( x, y). Then by the Midpoint Formula,
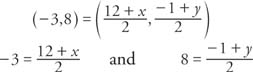
Multiply each side of each equation by 2.
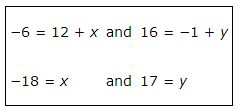
Therefore, the coordinates of B are (−18, 17).